Ejemplo solución de ED mediante series de potencia, punto singular

Ejemplo 1:

Encuentre la solución general de la siguiente ecuación diferencial en torno a x_0=0, indicando el intervalo de convergencia:

xy''(x) + 2y'(x) + xy(x) = 0

Solución:

Primero que todo, analizamos en la E.D los puntos ordinarios o singulares.  Si la E.D se escribe en la forma canónica: y''+p(x)y'+q(x)=0 , entonces puede verse que p(x)=2/x, q(x)=1,  por lo que el punto: x = 0 es la única singularidad de la ecuación diferencial y, además, es un punto singular regular.  Ya que el punto en torno al cual se hará la expansión en series de potencias es singular regular, entonces la solución tendrá la forma (Frobenius): y=\sum\limits_{k=0}^{\infty}c_k x^{k+\lambda} .

Ya que la discontinuidad más cercana al punto x_0=0 está en el infinito (x_s =\infty ), entonces el intervalo de convergencia de la serie es: 0<x-0<|0-\infty|, con lo cual:  0 <x<+\infty

Para solucionar la ED procedemos a derivar la solución propuesta y reemplazar en la ED, obteniendo:

x\sum\limits_{k=0}^{\infty}(k+\lambda)(k+\lambda-1)c_k x^{k+\lambda-2}+ 2\sum\limits_{k=0}^{\infty}(k+\lambda)c_k x^{k+\lambda-1} +x\sum\limits_{k=0}^{\infty}c_k x^{k+\lambda} \equiv 0 .

\sum\limits_{k=0}^{\infty}(k+\lambda)(k+\lambda-1)c_k x^{k+\lambda-1}+ \sum\limits_{k=0}^{\infty}(k+\lambda)2c_k x^{k+\lambda-1} +\sum\limits_{k=0}^{\infty}c_k x^{k+\lambda+1} \equiv 0 .

\sum\limits_{k=0}^{\infty}(k+\lambda)[k+\lambda-1+2]c_k x^{k+\lambda-1} +\sum\limits_{k=0}^{\infty}c_k x^{k+\lambda+1} \equiv 0 .

\sum\limits_{k=0}^{\infty}(k+\lambda)(k+\lambda+1)c_k x^{k+\lambda-1} +\sum\limits_{k=0}^{\infty}c_k x^{k+\lambda+1} \equiv 0 .

Expandiendo dos términos en la primera serie, nos queda:

\lambda(\lambda+1)c_0x^{\lambda-1}+(\lambda+1)(\lambda+2)c_1x^{\lambda}+ \sum\limits_{k=2}^{\infty}(k+\lambda)(k+\lambda+1)c_k x^{k+\lambda-1} +\sum\limits_{k=0}^{\infty}c_k x^{k+\lambda+1} \equiv 0

Realizando el cambio de variable: n=k-1 en la primera serie y n=k+1 en la segunda, se obtiene:

\lambda(\lambda+1)c_0x^{\lambda-1}+(\lambda+1)(\lambda+2)c_1x^{\lambda}+ \sum\limits_{n=1}^{\infty}(n+\lambda+1)(n+\lambda+2)c_{n+1} x^{n+\lambda} +\sum\limits_{n=1}^{\infty}c_{n-1} x^{n+\lambda} \equiv 0

\lambda(\lambda+1)c_0x^{\lambda-1}+(\lambda+1)(\lambda+2)c_1x^{\lambda}+ \sum\limits_{n=1}^{\infty}[(n+\lambda+1)(n+\lambda+2)c_{n+1}+c_{n-1}] x^{n+\lambda} \equiv 0

De aquí se infiere que la ecuación indicial es: \lambda(\lambda+1)c_0x^{-1}+(\lambda+1)(\lambda+2)c_1=0

Y la ecuación de recurrencia es: (n+\lambda+1)(n+\lambda+2)c_{n+1}+c_{n-1}=0 para n=1,2,..

Observando la ecuación indicial, podemos ver que si c_0 \neq 0 y c_1=0 se obtienen dos valores \lambda=0, \lambda=-1.  Las raíces difieren en un entero: 0-(-1)=1 por lo que la mayor de ellas garantiza UNA solución.  Sin embargo, es claro que la menor de ellas \lambda=-1 permite adicionalmente que c_1 \neq 0.  Esto implica que la escogencia de la raíz menor permite encontrar DOS soluciones.

Tomando la raíz menor 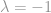\lambda=-1:

La ecuación de recurrencia nos queda: c_{n+1}=-\dfrac{c_{n-1}}{n(n+1)} para n=1,2,.. y c_0,c_1 \neq 0.

Asignando valores, resulta:

c_2 = -\dfrac{c_0}{2}
c_3 = -\dfrac{c_1}{3!}
c_4 = -\dfrac{c_2}{3\cdot 4} = \dfrac{c_0}{4!}
c_5 = -\dfrac{c_3}{4\cdot 5} = \dfrac{c_1}{5!}
c_6 = -\dfrac{c_4}{5\cdot 6} = -\dfrac{c_0}{6!}

Y así sucesivamente.  Con esto se obtiene la solución:

y(x)= x^{-1} \left[ c_0\left( 1-\dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \cdots \right) + c_1\left( x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} -\dfrac{x^7}{7!} + \cdots \right) \right]

Recordando las series de potencia para la función seno y coseno, podemos escribir la solución como:

y=c_0 x^{-1}\cos(x)+c_1 x^{-1}\sin(x)

Es claro que la escogencia de la menor de las raíces de la ecuación indicial condujo a la obtención de las dos soluciones de la ED, como se había descrito arriba.

Tomando la raíz mayor \lambda=0:

La ecuación de recurrencia nos queda: c_{n+1}=-\dfrac{c_{n-1}}{(n+1)(n+2)} para n=1,2,.. y c_0 \neq 0, c_1=0.

Asignando valores, resulta:

c_2 = -\dfrac{c_0}{2(3)}=-\dfrac{c_0}{3!}
c_3 = -\dfrac{c_1}{3(4)}=0
c_4 = -\dfrac{c_2}{4(5)} = \dfrac{c_0}{5!}
c_5 = -\dfrac{c_3}{5(6)} = 0
c_6 = -\dfrac{c_4}{6(7)} =- \dfrac{c_0}{7!}

Y así sucesivamente.  Con esto se obtiene la solución:

y(x)= x^{0} c_0\left( 1-\dfrac{x^2}{3!} + \dfrac{x^4}{5!} - \dfrac{x^5}{7!} + \cdots \right)

La cual se puede escribir como:

y(x)= x^{-1} c_0\left( x-\dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^6}{7!} + \cdots \right)

y(x)=x^{-1}c_0 \sin(x)

Como se indicó arriba, al usar la mayor de las raíces se garantiza UNA solución de la E.D.  La otra solución se puede encontrar usando el método de reducción de orden, así:

\phi=y_1^2 e^{\int{p(x)}dx}=y_1^2 e^{2\int{dx/x}}=y_1^2 e^{2\ln(x)}=y_1^2 x^2=x^{-2}\sin(x)^2 x^2 = \sin(x)^2

y_2=y_1\int{\phi^{-1}}dx=y_1\int{\sin(x)^{-2}}dx=y_1\int{\csc(x)^2}dx=y_1(-\cot(x))=-x^{-1}\sin(x) \dfrac{\cos(x)}{\sin(x)}=-x^{-1}\cos(x)

Con lo cual: y_2=x^{-1}\cos(x).  Que corresponde a la hallada anteriormente.

Deja un comentario